Power Flow: Remote Voltage Regulation

 

This is a subtopic of the Power Flow Solution Theory Help.

 

More complicated situations occur when generators are configured to regulate a bus that is not the terminal bus and when groups of generators coordinate their Mvar outputs to regulate a single remote bus together. This is depicted in the next image where there are three generators at buses A, B, and C which are working together to regulate the voltage at the regulated bus R.

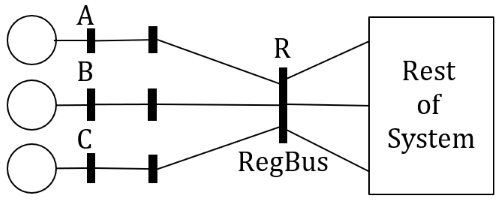
The proportion of total Mvars output by each of these generators is impacted by the user-designed option Sharing of generator Vars across groups of buses during remote regulation which is available on the Advanced Options tab of the Power Flow Solution Options on the Simulator Options Dialog. Examples that use the regulation factors will make use of user-enterable remote regulation factor (RegFactor) that is defined for each generator. The RegFactor values are then normalized to determine what relative amount of Mvar output from each generator is expected. Thus if generator A RegFactor was 10, B was 6, and C was 4, then you would expect generator A to have 2.5 times as much Mvar output as generator C and generator B would have 1.5 times as much Mvar output as generator C. A more complete description of how Mvars are shared between generators is available in another topic.

In order to enforce this kind of control the equations solved for are modified. Out of the buses that are participating in remote generator voltage regulation, one bus is chosen as the Primary Bus. For our example, let's assume that Bus A is chosen as the Primary Bus. All buses will enforce the real power flow summation to zero at the bus, but the reactive or voltage equations are then implemented as follows

 

Which Bus

Voltage or Reactive Equation Description

BusCat String
 

Bus A

As the primary bus it will enforce the bus voltage equation at the regulated Bus R

PV (Remote Reg Primary)

 

Bus B

and

Bus C

As secondary buses they will enforce an equation then ensures that the total Mvar output of generators at the respective bus is equal to the appropriate proportion of the summation of the Mvar outputs at Bus A, B and C (click link for more information on Mvar Sharing)

PQ (Remote Reg Secondary)

 

Bus R

The regulated bus will just enforce the reactive power flow summation at its bus.

PQ (Remotely Regulated)

Notice that the regulated bus is denoted as "PQ" even though the voltage at the regulated bus is being controlled. The equation that is enforcing the regulated bus voltage is instead coming from the primary Bus A. In this set equations the primary bus A has only 1 equation (P) while the regulated bus R has 3 equations (P, Q, and V). The unknown variables at all the buses here remain the variables V and d. Thus there are still have an equal number equations and unknown variables to solve for.

There are also 2 other possible BusCat strings related to remote regulation which are as follows